Razones y Proporciones.
 El concepto de razón y proporción es uno de los
más intuitivos de la matemática y aparece en diversos contextos y situaciones, por ejemplo en la relación gasto/compra, en la de espacio/velocidad....
La formalización de la teoría matemática de las razones y proporciones es debida a los griegos y en concreto a la escuela pitagórica, aunque se tienen noticias de ser utilizada por civilizaciones anteriores como la egipcia y la babilónica.
En la actualidad, esta teoría impregna numerosos ámbitos de la vida cotidiana y científica. En la vida cotidiana, podemos encontrarla en los descuentos, intereses bancarios, nóminas, IVA, en la misma tienda, supermercado, etc. Dentro
del ámbito científico, las relaciones de proporcionalidad se encuentran con gran frecuencia en la mayoría de las leyes de la Naturaleza: velocidad de un objeto en movimiento uniforme, relación entre presión, volumen y temperatura de
un gas, etc.
Razón es el resultado de comparar dos cantidades. Dos cantidades pueden compararse de dos maneras: Hallando en cuánto excede una a la otra, es decir, restándolas, o hallar cuantas veces contiene una a la otra, es decir, dividiéndolas.
De aquí que existan dos clases de razones: razón aritmética o por diferencia y razón geométrica o por cociente.
Los antiguos griegos creían que la proporción era esencial para conseguir belleza. Por eso estudiaron las
proporciones geométricas y algunas especiales, como la razón áurea, como veremos a continuación.
Proporción áurea.
La divina proporción o proporción áurea, expresada mediante el número de oro (Ф), se encuentra escondida en
numerosos elementos de la naturaleza como las conchas de los moluscos, la ramificación de los árboles, la configuración de las hojas en los tallos de las plantas, las pipas de los
girasoles o en la conformación del nautilus e incluso en la configuración de las galaxias espirales. Ya desde la antigüedad este fenómeno no pasó
inadvertido y fue estudiado por los matemáticos, científicos y artistas más importantes
de todas las épocas. Su pretensión no sólo era descubrir los secretos de esta proporción sino también aplicarla a sus propias creaciones para alcanzar así la belleza ideal, las obras más armónicas y perfectas que pudieran concebirse.
Los egipcios descubrieron la proporción áurea por análisis y observación del entorno, sin embargo su hallazgo escrito data de la Grecia clásica y el primer libro en donde aparece mencionado es en “Los elementos de Euclides”
(S. IV - III a.c.), libro fundamental para la geometría y las matemáticas en general ya que constituye una enciclopedia de los axiomas, principios y saberes de las matemáticas. Euclides habló de un punto que dividía un segmento de
recta en dos segmentos desiguales, de tal forma que este punto estuviese situado donde crease una misma proporción entre el segmento mayor y el menor y entre el total del segmento y el mayor, es decir, que “el todo es a la parte como la parte es al resto”.
Euclides en su obra le llama “extrema y media razón”, Luca Pacioli en el S. XV es quien lo nombra “divina proporción”, mientras que Leonardo da Vinci lo denomina “número de oro” y, ya en el S. XX, Mark Barr propone llamarlo
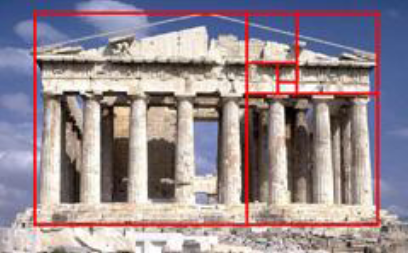
phi (Ф) en honor al arquitecto griego Fidias (Phidias), constructor del Partenón de Atenas. Ahora bien, un rectángulo áureo se dice es armónico si sus lados están en proporción áurea, es decir, a razón (1 : Ф). Este rectángulo aparece
en muchos fenómenos naturales, diversas creaciones artísticas y antiguas construcciones.
Para encontrar el número de oro (Ф), comenzaremos por dividir un segmento de recta cualquiera en dos partes desiguales de la forma más general y directa posible. Dado el segmento AB
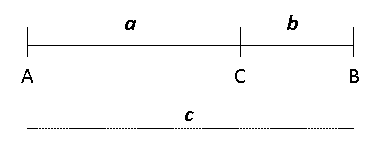
podemos formar seis razones con las medidas a, b, c. Después de estudiar los quince casos posibles de proporción que se pueden formar igualando dos razones cualesquiera de ellas, se llega a la conclusión de que dicha división,
llamada extrema y media razón por Euclides, consiste en hacer que el segmento mayor “a” sea al menor “b” como el total del segmento de recta “c” es al mayor “a”.
Es decir, la proporción divina está dada por:
$$ \frac{a}{b} = \frac{a+b}{a} $$
Si denotamos a la razón áurea $$ \frac{a}{b} =x$$ , entonces:
$$ x^{2}-x-1=0 $$ Ecuación cuadrática de la forma $$ Ax^{2}+Bx+C=0 $$
Las soluciones de esta ecuación de segundo grado son (compruébalo):
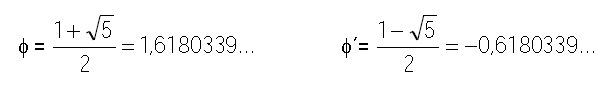
Debido a que los griegos sólo conocían los números racionales (cociente de dos números enteros), les dejó
perplejos encontrarse con los números $$ \sqrt{2} $$ (es la medida de la diagonal de un cuadrado de lado 1) y $$ \frac{1+\sqrt{5}}{2}
$$ que no podían escribirse como cociente de números enteros. A estos extraños números para ellos les llamaron irracionales.
El número de oro posee curiosas e importantes propiedades matemáticas. Como muestra señalaremos que:
$$ \Phi \cdot \Phi^{'}= - 1 $$
$$ \Phi + \Phi^{'}= 1 $$
(Compruébalo.)
De tal forma que si a este número se le disminuye en 1 se convierte en su recíproco, es decir:
$$ \Phi -1= \frac{1}{ \Phi } $$
siendo este el único número que verifica esta propiedad.
Profesor: Osman Villanueva García
Educación como Arte del desarrollo...
Visitanos en
|
