¿Podemos estudiar y tratar esa cosa llamada
AMOR utilizando MATEMÁTICAS?
Por Osman Villanueva García
Desde que el cálculo diferencial fue introducido en el último cuarto del siglo XVII por Newton y Leibniz, los fenómenos dinámicos en la física, biología, economía y todas las demás ciencias han sido extensamente estudiados mediante ecuaciones diferenciales. Sorpresivamente, uno de los problemas más importantes que concierne a nuestras vidas, la dinámica del enamoramiento, apenas comienza a tratarse desde este punto de vista[1].
El diseño de este problema se sustenta en el artículo publicado por S. Rinaldi [3] sobre el análisis de un modelo basado en ecuaciones diferenciales, que pretende describir la dinámica del enamoramiento entre dos individuos mediante la descripción de sus personalidades. El modelo hace referencia directa al caso particular ampliamente conocido del amor no correspondido.
La labor de Rinaldi fue motivada por el estudio desarrollado por F. Jones [4] en “El Cancionero” de Petrarca, uno de los libros de poemas de amor más célebres del mundo occidental. Un detallado análisis lingüístico y estilístico de todos los poemas fechados dirigidos por Petrarca a su amada Laura (ver Figura 1) ha permitido a Jones conjeturar que las emociones del poeta siguen un patrón cíclico bastante regular de aproximadamente 20 años, delimitado en sus extremos por el éxtasis y la desesperación. Basándose en esta conjetura, Jones fue capaz de organizar todos los poemas no fechados en orden cronológico, y entonces mostrar que el estilo lírico de Petrarca había evolucionado desde las prácticas medievales simbólicas tempranas al humanismo moderno y los modos artísticos de pensamiento y expresión.

Figura 1. Petrarca y Laura. Anónimo.
Si bien el trabajo de Rinaldi es completamente independiente del realizado por Jones, sí le da un fuerte sustento a sus descubrimientos. De hecho, para valores adecuados de los parámetros del comportamiento de Laura y de Petrarca, el modelo matemático presenta un atractor[2] único. Las condiciones requeridas para la existencia de tal atractor son fácilmente interpretables y concordantes con el retrato relativamente claro de estas dos personalidades que emerge de El Cancionero.
Francisco Petrarca (1304-1374), quizá el mayor poeta enfermo de amor de todos los tiempos, es el autor de El Cancionero, una colección de 366 poemas (sonetos, canciones, sextinas, baladas y madrigales). En Aviñón, a la edad de 23 años, él conoce a Laura, una hermosa dama casada de la cual queda completamente prendado. Sin lugar a dudas[3], puede decirse que la fecha fundamental del poeta, consignada por él mismo en un memorable soneto y recordada, de diversa forma, en tantos otros, fue el seis de abril de 1327, día de Viernes Santo. En la iglesia de Santa Clara, el poeta ve por primera vez a la mujer que había de inspirar sus rimas amorosas a lo largo de la vida entera. Aquella mujer se llamaba Laura, y, según nos dice el propio Petrarca, los encuentros entre ambos fueron poquísimos y casuales, y el amor jamás correspondido. La pretensión de que <<Laura>> no fuera otra cosa que una imagen ideal, una entidad simbólica, una alusión metafísica, teológica o, peor aún, críptica, ha tenido alterna fortuna a través de los siglos; pero en verdad, semejante interpretación es un atentado contra la verdad histórica y el sentido común. Laura fue una mujer de carne y hueso, feliz esposa de un gentil hombre y madre de nada menos que once hijos, arrebatada de este mundo por la peste en 1348. Esto es, en sentido estricto, todo lo que de ella sabemos en cuanto a biografía. Como tema poético, Laura es un privilegiado objeto de la más rica, sutil y constante poesía amorosa que se pueda imaginar.
A partir de aquella primera vez en que se enamoró de Laura y a pesar de que nunca fue correspondido, Petrarca le dedicó a ella más de 200 poemas durante los siguientes 21 años. Los poemas expresan instantes de pasión y desesperación, de desaires y reconciliaciones, y representan el nacimiento de la moderna poesía amorosa. Esta obra ha influenciado a incontables poetas, e incluso al mismo Shakespeare.
Desafortunadamente, sólo unos cuantos de los poemas de El Cancionero están fechados; el resto están clasificados en un orden desconcertantemente oscuro. El conocimiento del correcto orden cronológico de los poemas en un prerrequisito para el estudio de la evolución lírica, psicológica y estilística de cualquier poeta. Este hecho es particularmente importante en Petrarca, quién de alguna manera representa o, al menos, caracteriza la espectacular transición de la Edad Media al Humanismo. Por esta razón, la identificación del orden cronológico de los poemas de El Cancionero ha sido por siglos un problema de enorme interés para los eruditos.
F. Jones ha descrito en su libro cómo ha resuelto el problema del ordenamiento de estos poemas. Primero, él ha notado que en cierto número de versos Petrarca hace referencia recurrente a la naturaleza de su experiencia amorosa. Por ejemplo, en el soneto LXXVI[4] dice:
Amor con sue promesse lusinando Amor con sus promesas lisonjeando
mi ricondusse a la prigione antica, volvió a llevarme a la prisión antigua,
. . . . . .
mientras que en el soneto CCXXI él escribe:
Qual mio destìn, qual forza o qual inganno, ¿Qué destino, qué fuerza o cuál engaño,
mi riconduce disarmato al campo, vuelve a llevarme desarmado al campo
là ‘ve sempre son vinto? e s’io ne scampo, en que siempre soy derrotado? Y si me salvo,
. . . . . .
Asimismo, la actitud de Laura recurrentemente es menos inexorable. Por ejemplo, en la balada CXLIX Petrarca dice:
Di tempo in tempo mi si fa men dura De vez en cuando se vuelve para mí menos dura
l’angelica figura, e ‘l dolce riso, la angélica figura, y la dulce risa,
e l’aria del bel viso y la expresión del bello rostro
e de gli occhi leggiadri meno oscura. y de los agraciados ojos menos oscura.
. . . . . .
Modelo matemático de Laura y Petrarca.
Para modelar con matemáticas las emociones de Laura y Petrarca hacemos uso de un sistema de tres ecuaciones diferenciales ordinarias (ver Figura 2). Mediante la variable L(t) se representa el amor que siente Laura por el poeta al tiempo t. Valores positivos y grandes representan amistad y simpatía, en tanto que los valores negativos estarán asociados con frialdad y oposición. Por otra parte, la personalidad de Petrarca es más compleja, por lo que en su descripción se ocuparán dos variables: P(t), que representa su sentimiento por Laura, y Z(t), su inspiración poética. Grandes valores de P indican niveles de paroxismo, en tanto que valores negativos significan desesperación.

Con la finalidad de determinar la evolución temporal de las tres variables señaladas L(t), P(t) y Z(t), procedemos a formular para cada una de ellas una ecuación diferencial[5] ordinaria (EDO) haciendo, respectivamente, uso de las siguientes suposiciones:
- Dado que el interés de Laura por Petrarca lejos de aumentar francamente iba en decremento, la variación temporal del sentimiento amoroso de la musa L(t) debería decrecer en relación directa a éste. Además, considere que dicha tasa es igual a un término dado por una función RL(P(t)), que cuantifica la reacción de Laura por el amor a Petrarca. Asimismo, dele algunos visos de esperanza a Petrarca, considerando que esa rapidez es proporcional a cierta atracción (física o intelectual) que él ejerce sobre Laura, que sea constante, y denótela como AP .
- Dado que el amor de Petrarca por Laura no era correspondido, la fascinación de él por ella eventualmente va desapareciendo con el tiempo, por lo que resulta pertinente considerar que la tasa del sentimiento amoroso del poeta P(t) también irá decreciendo proporcionalmente a éste. También tome en cuenta que la rapidez de su sentimiento es igual a un término dado por la función RP(L(t)), el cual cuantifica la reacción de Petrarca por el amor a Laura. Al igual que en el caso anterior, en esta ecuación diferencial se tendrá un término de atracción (ahora de ella hacia él), pero que no es constante y depende seguramente de la inspiración del poeta, es decir, AL(Z(t)).
- Por último, la indiferencia pertinaz mostrada por Laura terminará por mermar con el tiempo la inspiración del poeta, por lo que resulta aceptable considerar que la variación temporal de Z(t) decrece en proporción directa a ésta. Sin embargo, debe tomarse en consideración la situación de que ante algún atisbo de interés que pudiera mostrar Laura hacia Petrarca, dicha tasa será también directamente proporcional al sentimiento amoroso de él por ella P(t).
Por lo tanto el modelo matemático queda determinado por:
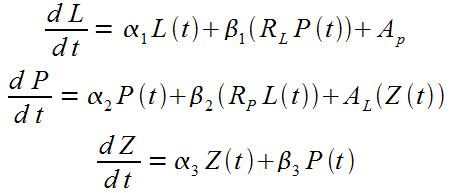
Figura 2. Sistema de EDO que representa el enamoramiento de Laura y Petrarca.
En donde las cantidades positivas α1, β1, α2, β2 y α3, β3 denotan a las constantes de proporcionalidad de cada uno de los términos indicados. A los parámetros αi se les denominan como de olvido, en tanto que a los βi, como de tipo reacción.
Referencias bibliográficas.
[1] S. H. Strogatz, Love affairs and differential equations. Math. Magazine, 61, p. 35 (1988).
[2] S. H. Strogatz, Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry and Engineering, Addison-Wesley (Reading, MA, 1994).
[3] S. Rinaldi, Laura and Petrarch: An Intriguing Case of Cyclical Love Dynamics, Siam J. Appl. Math. 58, 4, pp. 1205-1221, (1998).
[4] F. J. Jones, The Structure of Petrarch’s Canzoniere (Brewer, Cambridge UK, 1995).
[5] Petrarca, El Cancionero. Tomos I y II, cuarta edición. Edición bilingüe (Ediciones 29, Barcelona España, 1996).
¿Te gustó? ¡Compártelo en Twitter o Facebook!:
[1] Una excelente contribución ha sido el de S. H. Strogatz [1] [2], en la que propone un modelo simple sobre el romance entre Romeo y Julieta, el cual ha tenido bastante éxito en la enseñanza del
oscilador armónico.
[2] Desde el punto de vista físico- matemático se puede pensar como el conjunto al que el sistema evoluciona después de un tiempo suficientemente largo. Para que el conjunto sea un atractor, las trayectorias
del sistema que le sean suficientemente próximas han de permanecer próximas incluso si son ligeramente perturbadas. Ver http://es.wikipedia.org/wiki/Atractor
[3] Ver la introducción del tomo I de la edición bilingüe de El Cancionero [5].
[4] Los fragmentos de estos versos han sido obtenidos de la edición bilingüe (en latín y español) de El Cancionero de Petrarca [5].
Educación como Arte del desarrollo...
Visitanos en
|